Multiply-charged species
The bigger the molecule, the more likely it will be ionized multiple times in a Mass Spectrometer. Meaning more than one ion (e.g. in a positive mode: H⁺, Na⁺, [NH4]⁺) can attach to the analyte. They could be the same ion species (2H⁺) or different ones (H⁺Na⁺).
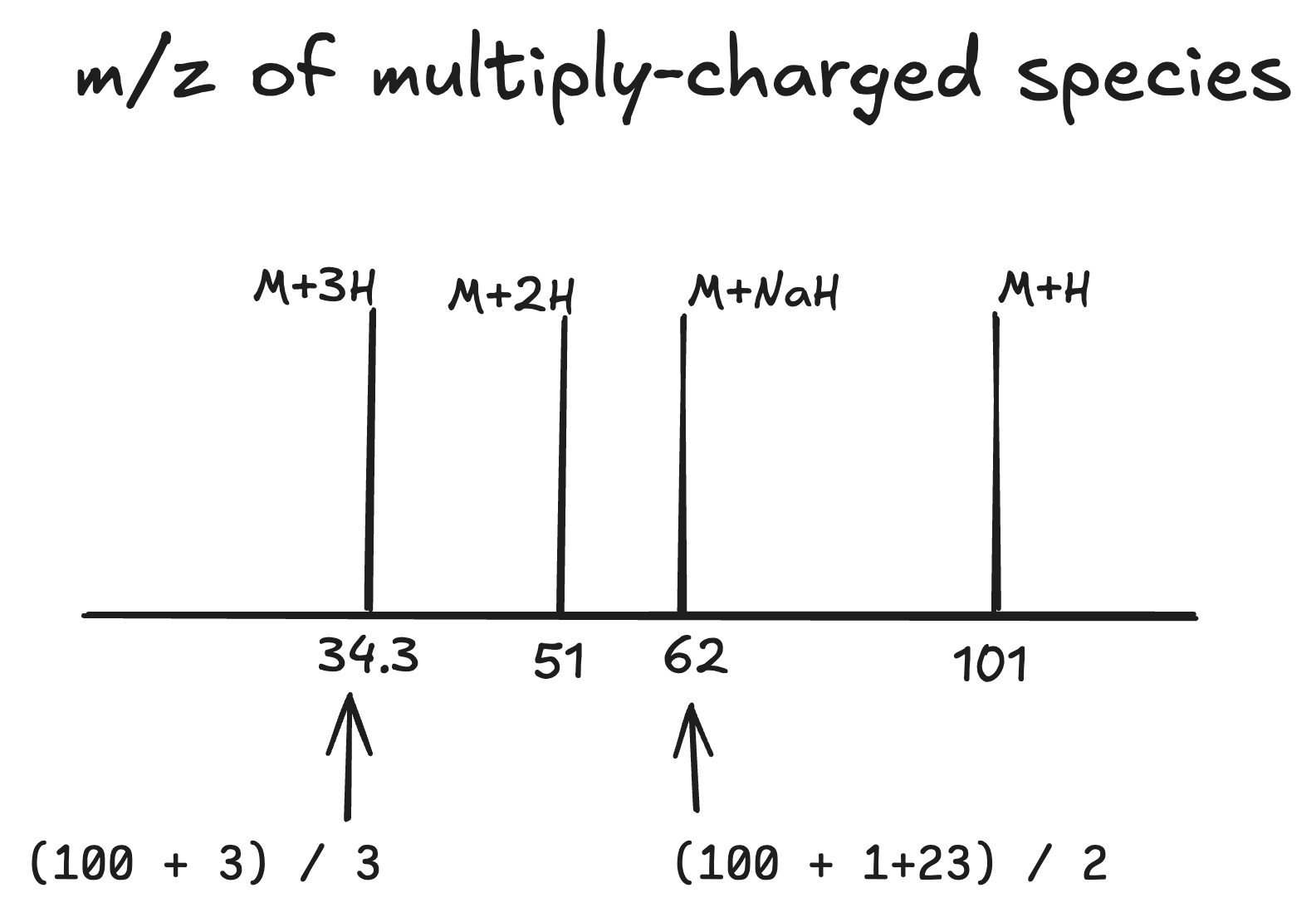
How does this look on a mass spectrum? Say our analyte is 100 Da, then:
-
A singly-charged species (M+H) has a mass 101 Da
-
A doubly-charged species (M+2H) has an even larger mass, however because its charge is doubled too, it will receive twice as much energy when electrical field is applied. This results in a mass:
(100Da + 2Da) / 2 = 51 m/z -
A triply-charged species (M+3H):
(100Da + 3Da) / 3 = 34.3 m/z -
A more complicated doubly-charged species (M+NaH):
(100Da + 1Da + 23Da) / 2 = 62 m/z
How many charges does my spectra show?
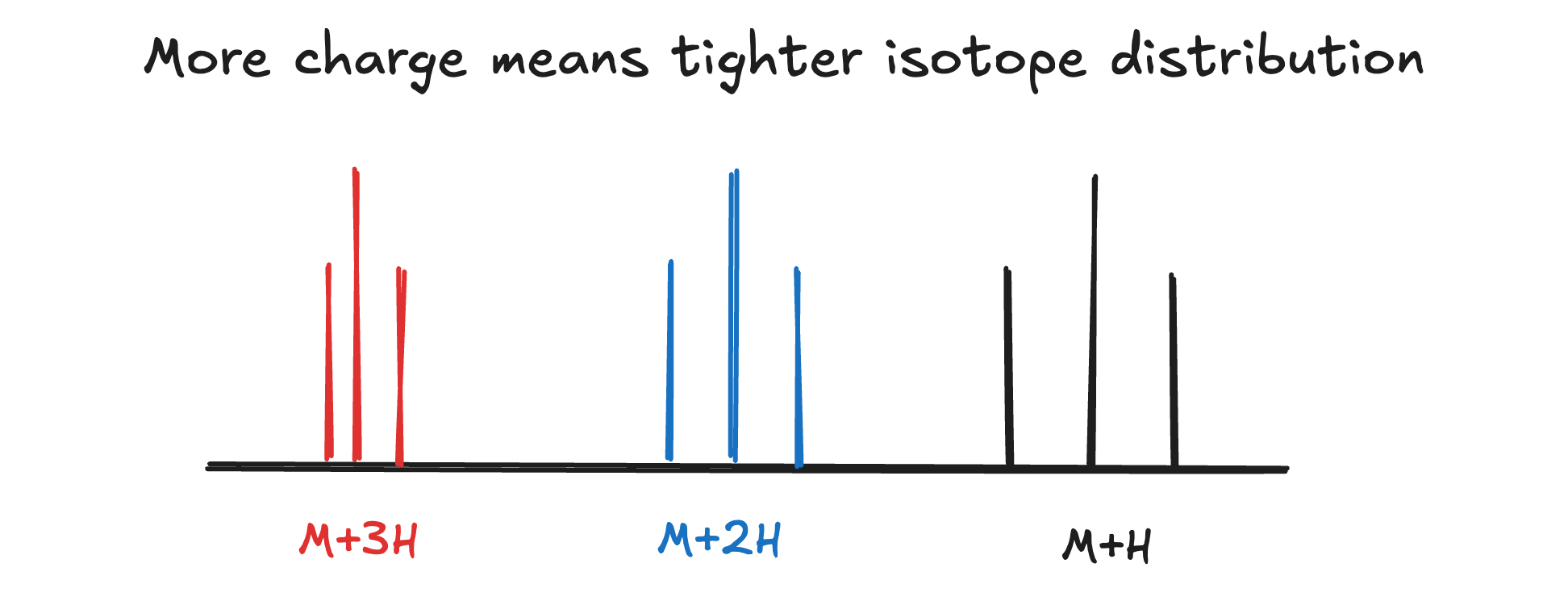
If you look at multiply-charged species, what you’ll notice is that the more charges there are the tighter the isotope distribution:
Why? Given our analyte M has isotopologues 100 and 102 Da:
-
M+H: 101 and 103
-
M+2H: 51 and 52 (102/2 and 104/2)
-
M+3H: 34.3 and 55 (103/3 and 105/3)
-
M+4H: 26 and 26.5 (104/4 and 106/4)
-
…
-
M+10H: 11 and 11.2 (110/10 and 112/10)
So while each ion adds to the constant in enumerator, it also increases the denominator. Both masses eventually converge to 1: ((M+∞)/∞ = 1).
When setting up adducts if you specify to
Max. count = 3, Peaksel will calculate the m/z for M+A, M+2A and M+3A. It
will look for all these ions in the mass spectra when extracting an EIC chromatogram.
Intensity of differently-charged species
If we know the composition of some adduct M+A, we can calculate the relative intensity of each isotopologue (ᵃ[M+A], ᵇ[M+A] and so on). And given the measured mass spectra we can confirm whether the pattern that we see conforms to the computations. This way we can confirm if we actually see our species or rather some other analyte with a similar mass (aka isobar). Peaksel does this for us.
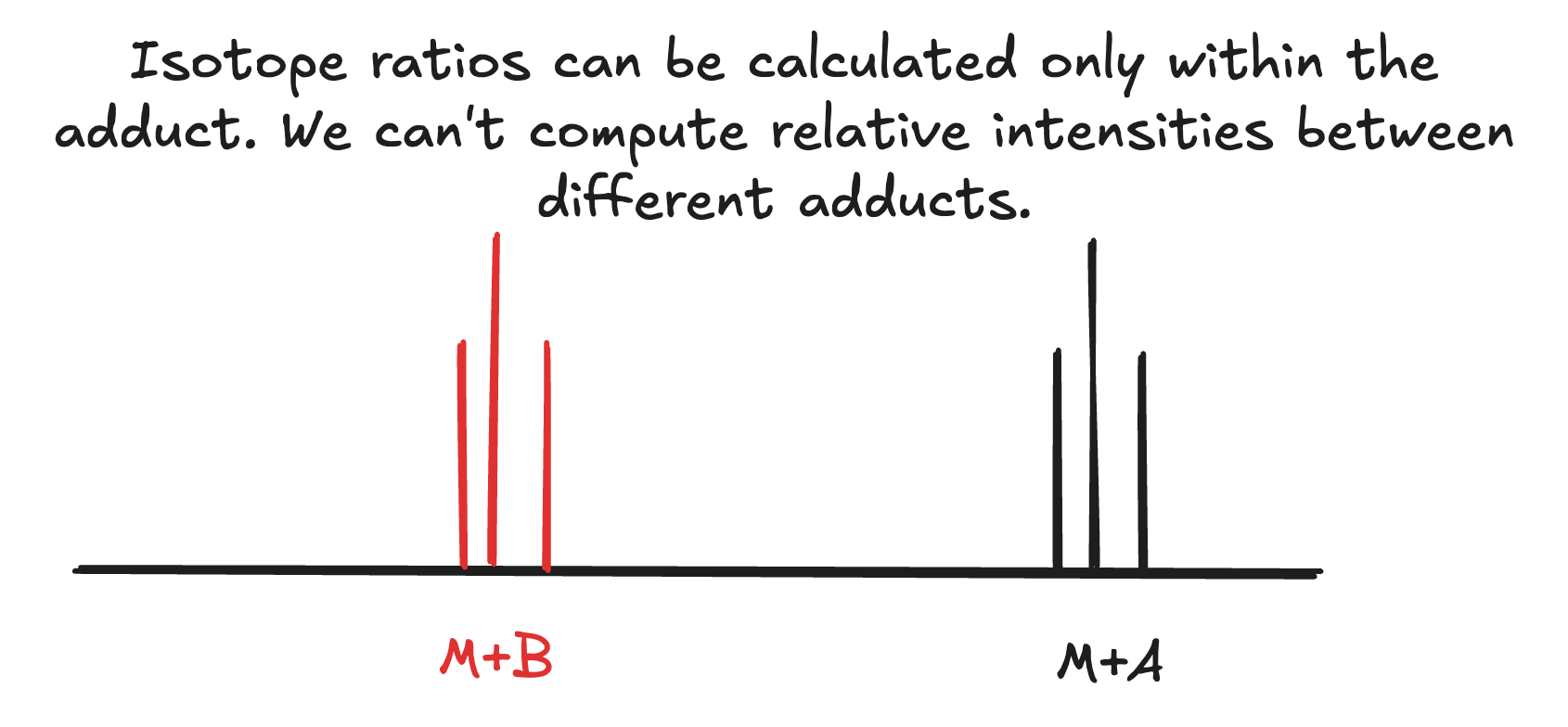
However, what if we have different adducts ([M+A], [M+B]), can calculate how the intensities of these are going to be related to each other? No, we can’t.
This is the reason why Peaksel shows you the theoretical distribution of isotopologues for each adduct separately. Each primary isotopologue within the adduct will have relative intensity of 100% exactly because we can’t predict which of them is more likely than the others.